[논문리뷰] LoRA: Low-Rank Adaptation of Large Language Models
이번에 리뷰할 논문은 모델 Efficency를 개선하는 측면 중 Parameter-Efficient Fine-Tuning (PEFT)에 근간이 될 수 있는 LoRA 논문에 대해 리뷰하려고 한다.
Background
Pre-trained 모델은 다양한 downstream task에 적용할 수 있다. 이러한 downstream task들은 pre-trained된 모델을 fine-tuning함으로써 성능을 높일 수 있다.
※ Dowmstream task? Summarization, Machine Reading Comprehension 등
그렇다면 fine-tuning은 어떠한 과정으로 이루어 지는것일까?
Fine-tuning과정에서 모델은 pre-trained된 weight를 초기화 한 다음, object function을 활용한다. 이 과정에서 대부분의 language model들은 maximum likelihood 문제로 풀었다. 즉, 입력된 context에 대해 다음에 어떤 token올지에 대한 최대의 가능성을 갖는 값을 찾는 것이다. 따라서 gradient descent에서 파생된 optimization function을 기반으로 우도를 측정한다.
우도를 측정하기 위해선 어떠한 요소들이 필요할까?
- backpropagation을 통해서 계산을 해야한다. 계산을 하기 위해선 값들은 텐서 안에 저장해 놓아야 한다.
- optimizer에서도 계산을 해야한다. 마찬가지로 계산을 하기 위해선 이전 이력들이 필요한 알고리즘의 경우 optimize state를 텐서 안에 저장해 놓아야 한다.
우도를 측정하기 위한 요소를 뿐만 아니라, GPT-3 같은 경우, 175B 파라미터 뿐만 아니라, 계산을 위한 텐서들도 저장해야한다. 하지만 요즘 추세를 보면 가용할 수 있는 하드웨어는 한정되어 있지만 모델은 점점 커지고 있는 추세이다.
따라서, 거대한 모델을 fine-tuning하기 위한 하나의 방법으로 LoRA라는 방식이 제안되었다.
기존에 제안되었던 방식들이 있었을까?
있었다면, 어떤 방식이었고 LoRA가 어떠한 측면에서 우수할까?
초기에 PEFT을 위해 제안되었던 방법은 Adapter를 사용하는 것이었다. 이때 Adapter란 기존에 이미 학습이 완료된 모델(pre-train model) 사이사이에 학습이 가능한 작은 feed-forward network를 삽입하는 구조를 말한다.
이때, pre-trained model의 weight는 고정시켜놓은 후 학습 가능한 작은 feed-forward network만 아키텍쳐 중간 중간마다 추가함으로써 적은 수의 파라미터로 튜닝하는 기법이다.
Adapter Layers Introduce Inference Latency
하지만, 기존에 제안되었던 방식의 경우 Inference Latency 이슈가 있다. 큰 모델의 경우 대기 시간을 늦추기 위해 병렬처리를 많이 활용했고, 이 방식은 adapter layer가 순서대로 처리되어야 하는 문제가 있기 때문이다. 따라서 adapter를 사용할 때 latency가 발생한다.
Directly Optimizing the Prompt is Hard
아예 Adapter를 활용하는 방식 말고, prefix tuning 방식도 있다. 하지만, 이 방식의 경우 optimize하기 어렵고, 성능이 학습가능한 파라미터마다 변동이 심한 문제점이 있다. 또한 downstream task에 적용할 경우, 활용할 수 있는 sequence length가 일부 줄어들게 된다.
하지만, 논문에서 제안한 LoRA의 경우 위에서 소개한 방식과 비교했을 때 large scale 모델에 적용할 수 있고, Inference Latency 문제를 해소했다는 장점이 있다.

LoRA
그렇다면 LoRA는 어떤 구조를 기반으로 학습이 진행되는지 알아보려고 한다.
기존의 full fine-tuning이라면 model은 pre-train model의 weight로 초기화 된 다음, 위에서 잠깐 설명한 것처럼 language model objective gradient를 최대화 하기 위해 전체 파라미터에 대해 지속적으로 업데이트를 해야한다.

따라서 본 논문에서는 parameter-efficient 방식을 통해 파라미터의 일부만 사용해 최적화 하는 방식을 제안했다.

LOW-RANK-PARAMETRIZED UPDATE MATRICES
- LoRA를 활용해 Pre-train weight를 고정된 상태로 유지하고
- Adaption 중 dense layer 변화에 대한 rank decomposition matrics를 최적화 하고
- 이를 통해서 신경망의 일부 dense layer를 간접적으로 훈련시키는 것이 가능하도록 했다.
따라서 학습할 수 있는 파라미터 수가 적고 inference latency와 학습 처리량이 높게 되었다. (RoBERTa의 경우 200개의 학습 가능한 파라미터로 90%의 퍼포먼스를 달성했다고 한다.)

이때, 위에서 언급했던 rank decomposition의 경우 그림처럼 행렬의 차원을 r만큼 줄이는 행렬과 다시 원래 크기로 키워주는 행렬의 곱으로 나타내는 것을 의미한다. 따라서 그림처럼 레이어 중간중간 hidden state에 값을 더해줄수 있는 파라미터를 추가해 모델의 출력 값을 원하는 타겟 레이블에 맞게 튜닝하는 것이 핵심이라고 볼 수 있다.
좀 더 구체적으로 설명하자면, 본 논문은 가중치에 대한 update도 adaption중 intrinsic rank가 낮다라는 것을 가정하고 ∆W (누적된 gradient)를 rank 분해 행렬곱으로 표현하였다.

- W0 + ∆W = W0 + BA
- h = W0x + ∆Wx = W0x + BAx
- W0는 고정하여 gradient update를 수행하지 않고, A,B는 학습 가능한 파라미터로 A는 무작위 가우스, B는 0으로 초기화 한다.
Inference시 추가적인 Latency가 필요하지 않고 다른 task로 전환하고 싶을 경우 BA를 빼서 W0를 복원하고 다른 B'A'를 load해 작은 메모리 오버헤드로 빠르게 연산이 가능하다.
실험 결과

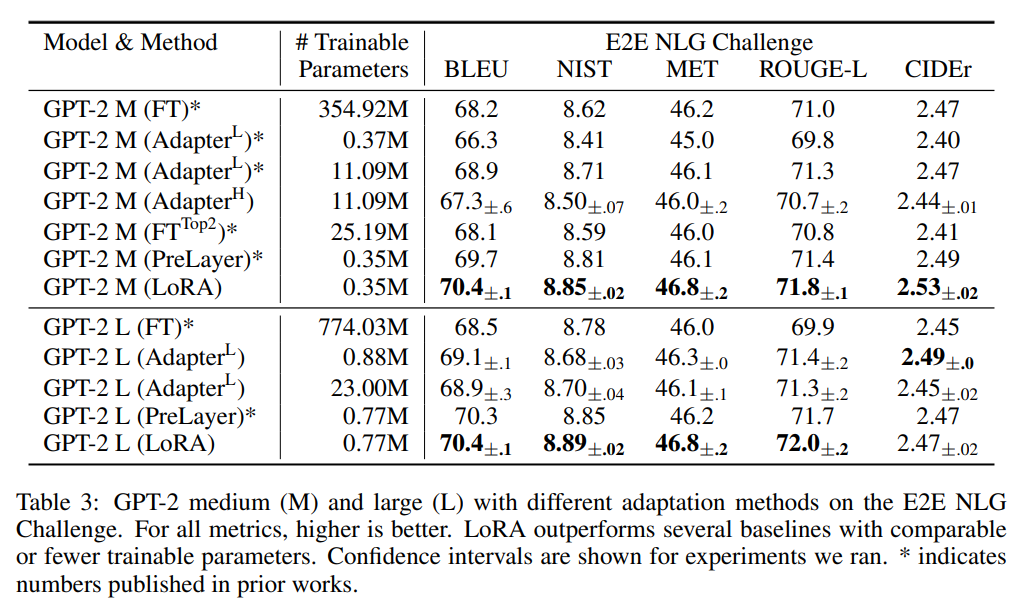
특히, NLU task에서 좋은 성능을 보이는 것을 볼 수 있다.
Experiment
어떤 가중치 행렬에 LoRA를 적용해야 하는지, LoRA를 위한 최적의 rank는 무엇인지에 대한 리포팅도 있다.
후기
최근들어 LLM이 쏟아져 나오고 있는데, 적은 파라미터에서 비슷한 성능을 내는 LoRA는 정말 강력하다고 볼 수 있다. 특히, 기존의 Adapter로 제안된 방법과 비교했을 때 inference latency도 들지 않고, sequence length를 줄일 필요도 없으며 사실상 dense layer라면 다 적용가능하다는 측면에 있어서 꼭 알아야 하는 기법 중 하나라고 생각한다.
또한, 요즘 추세를 보면 LoRA를 기반으로 QLoRA기법도 나오고 PEFT 연구도 활발하게 진행되고 있어 꼭 읽어봐야할 논문중 하나라고 생각한다.