Machine learning 모델에 기반한 Score모델을 평가할때 어떤 지표들을 활용할 수 있는지 정리해보고자 한다.
Score모델을 평가할 때 쓰이는 지표는 AUC, KS가 있다. 그리고 안정성을 평가하기 위한 지표로는 PSI가 있다.
오늘은 AUC에 대해 알아보려고 한다.
AUC (Area Under ROC)
AUROC의 의미는 ROC의 아래 영역이라는 뜻을 가진다. 따라서 AUROC에 들어가기 앞서 ROC에 대해 먼저 알아보고자 한다.
ROC 곡선
ROC곡선은 X축이 False Positive Rate(FPR), Y축이 True Positive Rate (TPR)인 그래프 위에 그려진다. 이해를 돕기위해, 예시를 들어 설명하고자 한다. 코로나에 대해 진단을 내린다고 할 때, 코로나가 걸렸을 경우 양성으로 진단하는 경우가 진양성, 코로나가 걸리지 않았는데 양성으로 진단(오진)하는 경우가 위양성이다. 반대로, 코로나가 걸리지 않았을 경우 음성으로 진단하는 경우가 진음성, 코로나가 걸렸는데 음성으로 오진하는 경우는 위음성이다.
실제 코로나 양성여부와, 진단 결과에서 각각 2가지 경우의 수가 있으므로 총 4가지 경우의 수가 존재하게 된다. 이 것은 아래와 같이 표로 정리할 수 있다.

위 개념을 기반으로 민감도(Sensitivity)와 특이도(Specificity)로 설명할 수 있다. 민감도는 코로나에 걸렸을 경우, 양성으로 진단하는 비율이며, 특이도는 코로나에 걸리지 않았는데 음성으로 진단하는 비율이다. 즉, 민감도와 특이도가 같이 높아야 진단의 정확도가 높다고 볼 수 있다.
- 민감도 (Sensitivity) = True Positive / (True Positive + False Negative)
- 특이도 (Specificity) = True Negative / (True Negative + False Positive)
위 개념을 기반으로 TPR과 FPR의 개념을 쉽게 파악할 수 있다.
- TPR (True Positive Rate) = Sensitivity
- FPR (False Positive Rate) = 1-Specificity
따라서 민감도와 특이도가 높은것은 곳 진단의 정확성이 높다는 것을 의미한다. 즉, TPR이 1에 가까울수록, FPR이 0에 가까울수록 유용한 것을 의미한다.
Decision Threshold
실제로 코로나 검사를 한다고, 민감도와 특이도가 모두 높게 나타나는 경우는 많지 않다. 따라서 민감도와 특이도 중 한 가지를 택하게 된다. 검사의 민감도를 높이면 전반적으로 양성으로 판단하는 비율이 높아지므로 위양성의 비율이 올라가게된다. 반대로 특이도를 높이게 되면 전반적으로 음성을 판단하는 비율이 높아지게 되므로 위음성의 비율이 높아지게 된다.
이때, 민감도 또는 특이도를 선택하는 판단 기준이 바로 Decision Threshold다. 즉, 결과 값이 얼마 이상일 때 양성으로 판단을 내릴지에 대한 기준이 필요하다. 왜냐하면, 판단 임계치가 높아지면 양성으로 판단하는 경우가 적어질 것이며, 반대의 경우 판단 임계치가 낮아지면 양성으로 판단하는 경우가 높아질 것이기 때문이다. 즉, 민감도를 확보하기 위해서는 Decision Threshold를 낮추어야 할 것이며, 특이도를 확보하기 위해서는 Decision Threshold를 높여야 할 것이다.
이해를 돕기 위해, Decision Threshold를 0 ~ 1.0 씩 0.1 간격으로 상승시켜 그때마다의 TP, FP, FN, TN을 계산해 TPR(민감도)과 FPR(1-특이도)을 다음과 같이 계산했다고 하자.

표와 같이, Decision Threshold가 0이면 무조건 양성으로 분류하게 되어 민감도가 100%가 되는것을 볼 수 있다.
ROC 곡선
위 표에 있는 (TPR, FPR) 쌍을 그래프에 하나씩 그려준다. 그 점들을 이어준 것이 바로 ROC 곡선이 된다.

이처럼 Decision Threshold에 대한 ROC곡선을 그린 후, 곡선에 대한 아래의 면적을 구한것이 AUC이다.
일반적으로 AUC 값은 0.5 ~ 1 사이의 값을 가진다. 1에 가까울수록 좋은 모델이다. 0.7 미만의 경우 차선(Sub-optimal)으로 고려할 수 있는 정도이며, 0.7~0.8은 좋은(Good)정도, 0.8 이상은 훌륭한(Excellent)정도로 볼 수 있다.
추가로 AUC 결과에 대해 자세하게 설명하자면,
1) AUC값이 1인 경우
- 두개의 TN (특이도), TP (민감도) 곡선이 겹쳐지지 않는 경우 모델은 이상적인 분류 성능을 보인다.
- 양성 클래스와 음성 클래스를 완벽하게 분류할 수 있다.

2) AUC값이 0.7인 경우
- 두 분포가 겹치면 'type 1 error (False Positive)', 'type 2 error (False Negative)'가 발생한다.
- 설정한 threshold에 따라, 위에 오류 값들을 최소화 또는 최대화 할 수 있다.
- AUC값이 0.7이면, 해당 분류 모델은 양성 클래스와 음성 클래스를 구별 할 수 있는 확률은 70%라는 것을 의미한다.

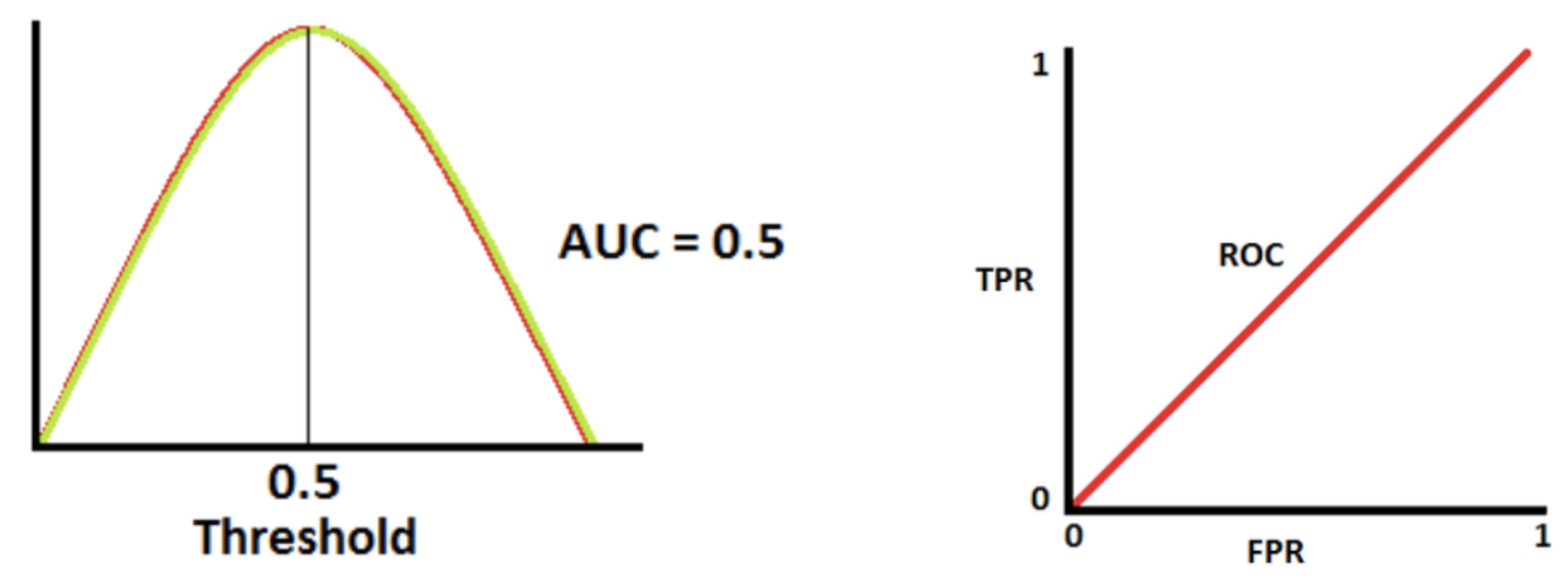
3) AUC값이 0.5인 경우
- 분류 모델의 성능이 최악인 것을 의미한다.
- 양성 클래스와 음성 클래스를 완벽하게 분류할 수 있는 능력이 없다.
Python 실습
학생 여부, 예치금액, 소득에 따라 채무를 이행했는지 여부를 분류하는 모델을 만들고자 한다. 모델은 RandomForestClassifier로 분류하려고 한다.
중요 패키지 import
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics
데이터 셋 load & RandomForest 모델 생성
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)
X = data[['student', 'balance', 'income']] # 학생인지, 예금, 소득
y = data['default'] # 채무 이행 여부
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
rf = RandomForestClassifier()
rf.fit(X_train,y_train)
AUC 계산
y_pred_proba = rf.predict_proba(X_test)[::,1]
fpr1, tpr1, thresholds = roc_curve(y_test, y_pred_proba, pos_label=1)
print("False Positive Rate: ", fpr1)
print("True Positive Rate: ", fpr1)
roc_auc1 = auc(fpr1, tpr1)
print("ROC : ", roc_auc1)
시각화
fig, ax = plt.subplots(figsize=(7.5, 7.5))
plt.plot(fpr1, tpr1, label='ROC Curve 1 (AUC = %0.2f)' % (roc_auc1))
plt.plot([0, 1], [0, 1], linestyle='--', color='red', label='Random Classifier')
plt.plot([0, 0, 1], [0, 1, 1], linestyle=':', color='green', label='Perfect Classifier')
plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.legend(loc="lower right")
plt.show()
Output
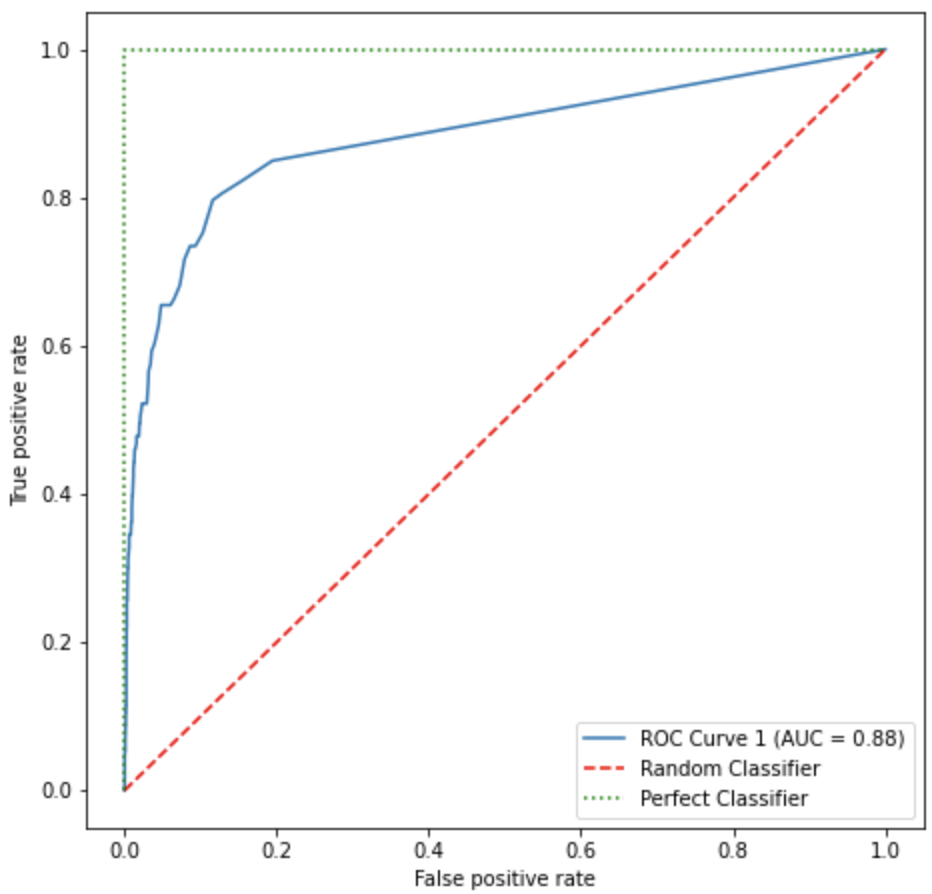
참고
댓글